Question

On a road trip you and your family stop a truck stop to take a break and to let your puppy Fido stretch. You notice that they have a triangular dog park that is fenced in on two sides. The third side of the field is formed by a creek. If the fences measure 150 feet and 98 feet, and the side along the creek is 172 feet, what are the measures of the angles made by the dog park?

Answer 1

cosine theorem can be used to calculate any of these three angles
cosα=(150^2+172^2-98^2)/2*150*172

Answer 2

Angles are 34.59°, 85.08° and 60.33°

Explanation:

Let ABC is a triangle, ( that show the dog park)

In which,

AB = 150 feet

BC = 98 feet

CA = 172 feet,

By the cosine law,

`BC^2=AB^2+AC^2-2(AB)(AC)cos A`

`2(AB)(AC)cos A=AB^2+AC^2-BC^2`

`\implies cos A=(AB^2+AC^2-BC^2)/(2(AB)(AC))-----(1)`

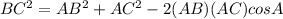
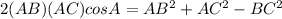
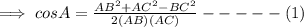
Similarly,

`\implies cos B=(AB^2+BC^2-AC^2)/(2(AB)(BC))-----(2)`

`\implies cos C=(BC^2+AC^2-AB^2)/(2(BC)(AC))-----(3)`

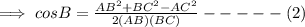
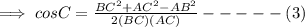
By substituting the values in equation (1),

`cos A=(150^2+172^2-98^2)/(2* 150* 172)`

`=(22500+29584-9604)/(51600)`

`=(42480)/(51600)`

`\approx 0.8233`

`\implies m\angle A\approx 34.59^(\circ)`

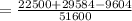
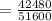
Similarly,

From equation (2) and (3),

m∠B ≈ 85.0°, m∠C ≈ 60.33°