30)
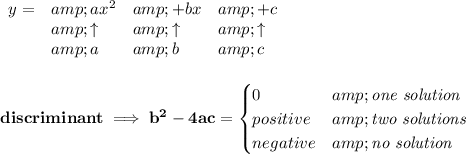
31)
a simple case for that would just be, using an equation with an imaginary value, let's do so
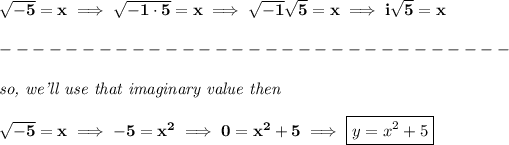
when you get a "solution" or zero with an "i" or an imaginary value, is just a way to say, there's really no solution, the function never touches the x-axis