Question

What is the number of square units in the area of the triangle whose vertices are points (2,0), (6,0), (8,5)

Answer 1

check the picture below

you can pretty much just count how many units for the base, and height.

Answer 2

Answer: 10 square units.

Explanation:

The area of triangle with vertices
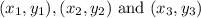`(x_1,y_1),(x_2,y_2)\text{ and }(x_3,y_3)` is given by :-

`A=(1)/(2)[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`

Given : The vertices of triangle : (2,0), (6,0), (8,5)

Then , the area of the triangle will be :_

`A=(1)/(2)[(2)((0)-(5))+(6)((5)-(0))+(8)((0)-(0))\\\\\Rightarrow A=(1)/(2)[20]\\\\\Rightarrow A=10\text{ square units}`

Hence, the number of square units in the area of the triangle whose vertices are points (2,0), (6,0), (8,5) = 10