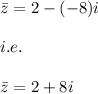Question

Which of the following is the conjugate of a complex number with 2 as the real part and −8 as the imaginary part?

Answer 1

The complex number is given as: 2-8i

So for conjugate, you just flip the sign of the imaginary part:

2+8i will be the answer

Answer 2

The conjugate of the given complex number is:

`2+8i`

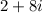
Explanation:

We know that any complex number is written in the form of:

`z=a+ib`

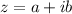
where a and b are real numbers.

The conjugate of the complex number is given by:

`\bar z=\bar {a+ib}\\\\i.e.\\\\\bar z=a-ib`

Here we are given that:

We have a complex number such that the real part of a complex number is 2 and it's imaginary part is -8.

i.e.

a=2 and b= -8

i.e. the complex number is:

`z=2+(-8)i`

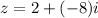
Hence, the conjugate of this number is:

`\bar z=2-(-8)i\\\\i.e.\\\\\bar z=2+8i`