Question

Andrew deposited $500 in a savings account that offers an interest rate of 6.5%, compounded continuously.

Andrew's initial deposit will grow to $543 in ___
months.

Answer 1

The formula is
A=pe^(r×t/12)
A future value 543
P present value 500
R interest rate 0.065
E constant
T time t ( in months)

Solve the formula for t
T/12=[log (A/p)÷log (e)]÷r
T/12=(log(543÷500)÷log(e))÷0.065
T/12=1.3
T=1.3×12
T=15 months

Answer 2

Time in months ≈ 16 months

Explanation:

Principal Amount = $500

Interest Rate = 6.5%

Amount = $543

n = Number of times the interest is compounded

⇒ n = 12 ( because given that the interest is compounded continuously)

We need to calculate Time in months :

`Amount=Principal* (1+(Rate)/(100* n))^(Time* n)\\\\\implies 543 = 500* (1+(6.5)/(100* 12))^(12* Time)\\\\\implies 1.086=(1.0054)^(12* Time)\\\\\text{Taking log on both the sides}\\\\\implies \log1.086 = 12* Time * \log 1.0054\\\\\implies 12 * Time=15.32\\\\\implies Time = 1.28\:\:years`

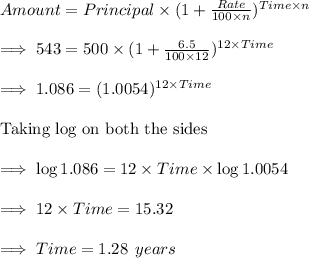
So, Time in months = 1.28 × 12

≈ 16 months