Final answer:
To find the nth term of the given geometric sequence, use An = 16 *
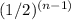 , reflecting that each term is half the preceding one.
, reflecting that each term is half the preceding one.
Step-by-step explanation:
The student is looking to generalize the sequence 16, 8, 4, 2, ... and find the nth term. This sequence is geometric, since each term is half the previous one, representing a common ratio of 1/2. To find the nth term of a geometric sequence, you can use the formula:
An = A1 *
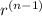
Where An is the nth term, A1 is the first term, r is the common ratio, and n is the term number. For this sequence with A1 = 16 and r = 1/2, the nth term is An = 16 *
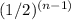 .
.