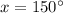Question

In the diagram below, AB is parallel to CD. What is the value of x?

Answer 1

x + 30 = 180
x = 180 - 30
x= 150

Answer 2

Option A is correct.

`x =150^(\circ)`

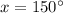
Explanation:

It is given that
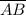`\overline{AB}` is parallel to
`\overline{CD}`

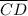
To find the value of x:

labelled the diagram as shown in the attachment:

`\angle DOQ = 30^(\circ)`

`\angle COE = \angle DOQ = 30^(\circ)` {Vertically opposite angle}

Corresponding angles theorem states: If two parallel lines are cut by a transversal, then the pairs of corresponding add up to 180 degree.

`x + 30^(\circ) = 180^(\circ)`

`x = 180 -30 = 150^(\circ)`

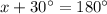
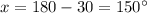
therefore, the value of
`x =150^(\circ)`