Question

When Carolyn drew the diagonals of parallelogram QRST, four triangles were formed as shown.

Which triangle(s) could Carolyn DEFINITELY show to be congruent to triangle QOT, when proving that the diagonals of the parallelogram bisect each other?

A)
only triangle SOR


B)
triangle SOR and triangle SOT


C)
triangle QOR and triangle SOR


D)
triangle QOR, triangle SOR, and triangle SOT

Answer 1

The correct answer is A) Only triangle SOR, because QOT and SOR have the same angles therefore in this parallelogram the two triangles are congruent.

Answer 2

Answer: A) only triangle SOR

Explanation:

Since, In parallelogram QRST,

When we take two traingles QOT and ROS,

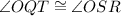`\angle OQT\cong \angle OSR` ( Because QR is parallel to TS and QS is the common transversal)

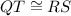`QT\cong RS` ( by the property of parallelogram)

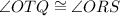`\angle OTQ\cong \angle ORS` ( Because QR is parallel to TS and RT is the common transversal)

Therefore by ASA postulate

`\triangle QOT\cong \triangle ROS`,

But, We can not say that triangle QOT is congruent to triangles SOT and QOR.

Therefore Only Option A) is correct.