Question

From a boat on the lake, the angle of elevation to the top of a cliff is 26°1'. If the base of the cliff is 205 feet from the boat, how high is the cliff (to the nearest foot)?

Answer 1

we use the tangent for this

tan 26 1 = opposite / adjacent = h / 205 where h = height of cliff

h = 205 tan 26 1 = 100 feet

Answer 2

Let the distance of the cliff from the boat be y and height of the top of the cliff be x.

As per the statement:

From a boat on the lake, the angle of elevation to the top of a cliff is 26°1'. If the base of the cliff is 205 feet from the boat.

⇒y = 205 feet,
`\theta =26^(\circ) 1'`

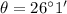
We have to find the high is the cliff i,e x.

Using tangent ratio:

`\tan \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}`

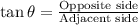
See the diagram as shown below:

Opposite side = x feet

adjacent side = 205 feet

Using conversion:

`1' = (1)/(60)^(\circ)`

then;

`\theta =26^(\circ) 1' = 26(1)/(60) = 26.017^(\circ)`

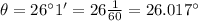
Substitute these values we have;

`\tan 26.017^(\circ) = (x)/(205)`

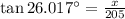
Multiply both sides by 205 we have;

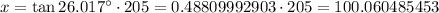`x = \tan 26.017^(\circ) \cdot 205 = 0.48809992903 \cdot 205 =100.060485453` ft

Therefore, 100 ft high is the cliff(to the nearest foot)