Answer:
B. Minimum at (3, –4)
Explanation:
Given is a quadratic function as

Considering the first two terms, we find that if we add 9 we can make it a perfect square
Hence add and subtract 9 to right side
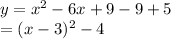
This is in vertex form
Vertex = (3,-4)
Since coefficient of leading term of x is positive, the parabola is open up and hence minimum is at (3,-4)
Option B,