Question

Describe how to simplify the expression 3^-6/3^-4

A. Divide the bases and then add the exponents.
B. Keep the base the same and then add the exponents.
C. Multiply the bases and then subtract the exponents.
d. Keep the base the same and then subtract the exponents.

Answer 1

Answer: d. Keep the base the same and then subtract the exponents.

Explanation:

The given expression:
`(3^(-6))/(3^(-4))`

According to the law of exponents in division with same base:-

`(a^m)/(a^n)=a^(m-n)`

In the given expression, both numerator and denominator has exponents wth the same base, hence to solve the expression we need to use law of exponents of division.

Hence, to simplify the
`(3^(-6))/(3^(-4))`, we need to keep the base the same and then subtract the exponents.

i.e
`(3^(-6))/(3^(-4))=(3)^(-6-(-4))=3^(-6+4)=3^(-2)`

Answer 2

(D)
`3^(-2)`

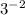
Explanation:

We have to simplify the given expression that is :

`(3^(-6) )/(3^(-4) )`

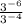
Now, keeping the base same and then subtracting the components, we have

first keep the base same,

`3^(-6){*}3^(-4)`

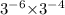
Now, subtract the exponents,

⇒
`3^(-6+4)`

⇒
`3^(-2)`

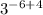
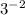
Which is the required simplified expression.

Therefore, Option D is correct.