Question

Which expression is equivalent to (x^-6/x^2)^3

Answer 1

Find the expression equivalent to

`= ((x^(-6))/(x^(2)))^(3)`

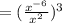
To prove

The expression given in the question be

`= ((x^(-6))/(x^(2)))^(3)`

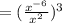
Now using the properties of the exponent.

The quotient of powers property and tells us that when you divide powers with the same base you just have to subtract the exponents.

i.e

`(x^(a))/(x^(b)) = x ^(a - b)`

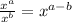
Apply this properties in the above

`= (x^(-6-2))^(3)`

`= (x^(-8))^(3)`

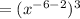
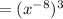
Now using the property

To find a power of a power you just have to multiply the exponents.

i.e

`(ab)^(2) = a^(2). b ^(2)`

Apply this property in the above

`= x^(-24)`

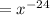
it is also written as

`= (1)/(x^(24))`

Answer 2

For this problem, just apply the laws of exponents. When dividing variable with the same base, just subtract their exponents. Hence, x^-6 divided by x^2 would be x^-8. Then, multiply the exponent with 3, becoming x^-24. Or, in reciprocal form, 1/x^24.