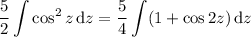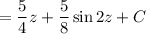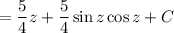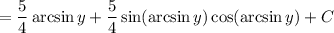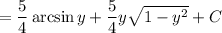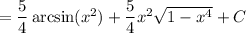Question

Integral of 5xsqrt1-x^4

Answer 1

`\displaystyle\int5x√(1-x^4)\,\mathrm dx`

Take
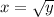
`x=\sqrt y`, so that
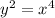
`y^2=x^4` and
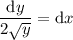
`(\mathrm dy)/(2\sqrt y)=\mathrm dx`. Note that this assumes
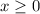
`x\ge0` and so requires
`y\ge0`.


`\displaystyle5\int\sqrt y√(1-y^2)(\mathrm dy)/(2\sqrt y)=\frac52\int√(1-y^2)\,\mathrm dy`

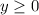
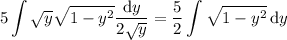
Now take
`y=\sin z`, so that
`z=\arcsin y`. Note that for this invertibility condition to hold, we require that
`-\frac\pi2\le z\le\frac\pi2`, which means
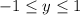
`-1\le y\le1`. But since we already fixed
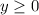
`y\ge0` with the previous substitution, we thus have
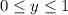
`0\le y\le1`, which in turn restricts us to
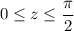
`0\le z\le\frac\pi2`. So with this substitution, we have
`\mathrm dy=\cos z\,\mathrm dz`, which gives


`\displaystyle\frac52\int√(1-\sin^2z)\cos z\,\mathrm dz`

`=\displaystyle\frac52\int√(\cos^2z)\cos z\,\mathrm dz`

`=\displaystyle\frac52\int|\cos z|\cos z\,\mathrm dz`

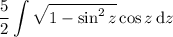
Now over the interval
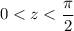
`0<z<\frac\pi2`, we have
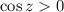
`\cos z>0`, which means
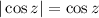
`|\cos z|=\cos z`, and so the integral is equivalent to


`\displaystyle\frac52\int\cos^2z\,\mathrm dz=\frac54\int(1+\cos2z)\,\mathrm dz`

`=\frac54z+\frac58\sin2z+C`

`=\frac54z+\frac54\sin z\cos z+C`

`=\frac54\arcsin y+\frac54\sin(\arcsin y)\cos(\arcsin y)+C`

`=\frac54\arcsin y+\frac54y√(1-y^2)+C`

`=\frac54\arcsin(x^2)+\frac54x^2√(1-x^4)+C`