Question

For a data set with a mean of 150 and a standard Deviation of 15, use chebyshev theorem to find the interval of which 75% of the data will fall.

Answer 1

The Chebychev's theorem states that for any numerical data set,
1.) at least
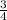
`(3)/(4)` of the data lie within two standard deviations of the mean;
2.) at least
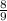`(8)/(9)` of the data lie within three standard deviations of the mean;
3.) at least
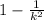`1-(1)/(k^2)` of the data lie within k standard deviations of the mean, where k is any positive whole number that is greater than 1.

Thus, given a data set with a mean of 150 and a standard Deviation of 15, 75% of the data represent
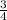`(3)/(4)` of the data, and according to Chebychev's theorem, at least
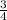`(3)/(4)` of the data lie within two standard deviations of the mean.

Thus, 75% of the data will fall within the interval

`150\pm2(15)=150\pm30=(150-30,\ 150+30)=(120,\ 180)`.

Therefore, 75% of the data will fall within the interval 120 to 180.