Question

Ti solve the system of equations below, Becca isolated x^2 in the first equation and then substituted it into the second equation. What was the resulting equation? (equation and choices in pic)

Answer 1

You isolate x^2 which makes it x^2=9-y^2
Then you substitute that into the second equations which gives you answer C!
Hope this helps

Answer 2

(C)
`(9-y^2)/(25)-(y^2)/(36)=1`

Explanation:

It is given that there is the system of the equations that are:

`x^2+y^2=9` (1)

and
`(x^2)/(25)-(y^2)/(36)=1` (2)

Becca isolated
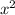`x^2` from the equation (1) and substituted in equation (2), therefore

From the equation (1), we have

`x^2=9-y^2`

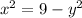
Substituting this in equation (2), we get

`(9-y^2)/(25)-(y^2)/(36)=1`

This is the resulting equation.

Thus, option C is correct.