Answer:
The nth term of the geometric sequence is given by;
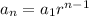 , .....[1] n is the number of terms.
, .....[1] n is the number of terms.
where,
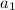 is the first term and r is the common ratio of the terms.
is the first term and r is the common ratio of the terms.
As per the statement:
Given:
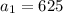 and
and
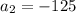
Using [1];

Substitute the value of
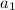 we have;
we have;

Divide both sides by 625 we have;
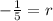
or
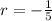
We have to find 7th term of the geometric sequence.
For n = 7 we have;

Substitute the given values we have;
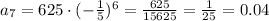
therefore, the 7th term of the geometric sequence is, 0.04