Question

For the following geometric sequence find the explicit formula.
{12, -6, 3, ...}

Answer 1

It's geometric sequence where
`a_1=12, q=-(1)/(2)`

So
`a_n=12\cdot\left(-(1)/(2)\right)^(n-1)`

Answer 2

`a_n=12*(-(1)/(2))^(n-1)`

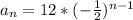
Explanation:

We are asked to write an explicit formula for the given geometric sequence.

We know that explicit formula for a given geometric sequence is in form
`a_n=a_1*r^(n-1)`, where,

`a_n=\text{ nth term of sequence}`,

`a_1=\text{ 1st term of sequence}`,

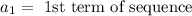`r` = Common ratio.

`n` = Number of terms of sequence.

To find common ratio, we will divide any term of our given sequence by its previous term.

`r=-(-6)/(12)=-(1)/(2)`

`a_n=12*(-(1)/(2))^(n-1)`

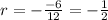
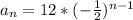
Therefore, our required formula would be
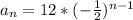`a_n=12*(-(1)/(2))^(n-1)`.