Question

A line has a slope of -3/5. Which ordered pairs could be points on a parallel line? Check all that apply.

(–8, 8) and (2, 2)
(–5, –1) and (0, 2)
(–3, 6) and (6, –9)
(–2, 1) and (3, –2)
(0, 2) and (5, 5)

Answer 1

(-2,1) and (3, -2) you can find this by calculating y2-y1 over x2-x1

Answer 2

Option A and D are correct

(–8, 8) and (2, 2), (–2, 1) and (3, –2)

Explanation:

Parallel line:

In parallel lines, the two lines have the same slope and will never intersects.

Using the slope formula:

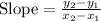`\text{Slope} = (y_2-y_1)/(x_2-x_1)` ....[1]

As per the statement:

A line has a slope of -3/5.

We have to find which ordered pairs could be points on a parallel line.

A.

(–8, 8) and (2, 2)

Substitute in [1] we have;

`\text{Slope} = (2-8)/(2-(-8))`

⇒
`\text{Slope} = (-6)/(10)= -(3)/(5)`

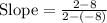
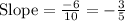
Similarly for:

B.

(–5, –1) and (0, 2)

Substitute in [1] we have;

`\text{Slope} = (2-(-1))/(0-(-5))`

⇒
`\text{Slope} = (3)/(5)= (3)/(5)`

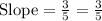
C.

(–3, 6) and (6, –9)

Substitute in [1] we have;

`\text{Slope} = (-9-6)/(6-(-3))`

⇒
`\text{Slope} = (-15)/(9)=- (5)/(3)`

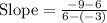
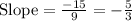
D.

(–2, 1) and (3, –2)

Substitute in [1] we have;

`\text{Slope} = (-2-1)/(3-(-2))`

⇒
`\text{Slope} = (-3)/(5)= -(3)/(5)`

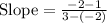
E.

(0, 2) and (5, 5)

Substitute in [1] we have;

`\text{Slope} = (5-2)/(5-0)`

⇒
`\text{Slope} = (3)/(5)=(3)/(5)`

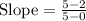
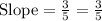
Therefore, the ordered pairs could be points on a parallel line are:

(–8, 8) and (2, 2)

(–2, 1) and (3, –2)