Question

Find the x-intercepts of the parabola with the vertex (4,-1) and y-intercept (0,15)

Answer 1

1. A parabola is the graph of the function


`y=f(x)=ax^2+bx+c`

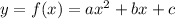
(0, 15 ) is a point of this parabola, so
`15=f(0)=a(0)^2+b(0)+c=c`

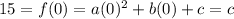
So c=15, which means we decrease the number of unknowns and write again:

`y=f(x)=ax^2+bx+15`

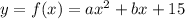
2. Now, since (4, -1) is another point in the parabola:


`-1=f(4)=a(4)^2+b(4)+15`
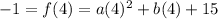
16a+4b=-16
dividing by 4:
4a+b=-4

We also know that -b/2a gives the x-coordinate of the vertex:

-b/2a=4
-b=8a
b=-8a

Substitute b=-8a in 4a+b=-4,
we get 4a-8a=-4
-4a=-4
a=1, then b=-8

So y=f(x)=x^2-8x+15

The roots of the expression, which are the x-intercepts can be found by solving the equation:


`x^2-8x+15=0`

`x^2-8x+16-1=0`

`(x-4)^2=1`

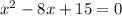
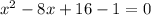
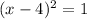
solution 1: x-4=1, x=5
solution 2: x-4=-1, x=3

The x-intercepts are (3, 0) and (5, 0)