Question

For a population, the mean is 19.4 and the standard deviation is 5.8. Compare the mean and standard deviation of the following random samples to the population parameters.

12, 15, 17, 20, 13, 11, 18, 19, 15, 14

Answer 1

The mean of the sample is 15.4 and the standard deviation of the sample is 2.87. This shows that the population parameters of the sample is lower and is less dispersed.

Answer 2

Mean is
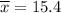`\overline{x} =15.4` and standard deviation is 3.02581485

Explanation:

Given mean is 19.4 and standard deviation is 5.8

the given data are: - 12, 15, 17, 20, 13, 11, 18, 19, 15, 14

Mean of given data is calculated as :-

`\overline{x} =(1)/(n)\sum_(i=1)^(n)x`

`\overline{x} =(12+15+17+20+13+11+18+19+15+14)/(10)`

`\overline{x} =(12+15+17+20+13+11+18+19+15+14)/(10)`

`\overline{x} =(154)/(10)`

`\overline{x} =15.4`

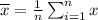
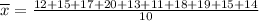
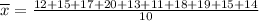
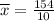
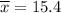
Mean is
`\overline{x} =15.4`

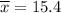
standard deviation is calculated as :-

`s=\sqrt{(1)/(n-1)\sum_(i=1)^(n)(x-\overline{x})^(2)`

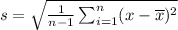
the sum of
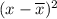`(x-\overline{x})^(2)` is performed in figure-1

`s=\sqrt{(1)/(10-1)\sum_(i=1)^(n)((412)/(5))`

`s=\sqrt{(1)/(9)*(412)/(5)`

`s=\sqrt{((412)/(45))`

`s=\sqrt{((412)/(45))`

`s=3.02581485`

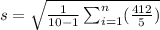
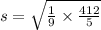
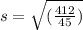
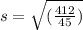
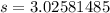
standard deviation is 3.02581485