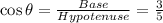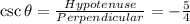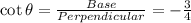Question

Sec theta = 5/3 and the terminal point determined by quadrant 4

Answer 1

cot theta = -3/4
-
sin theta = -4/5

Note - The - is just a spacer your not subtracting.

Answer 2

Here, we have
`\sec\theta =(5)/(3)`

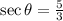
Since
`\sec\theta=(Hypotenuse)/(Base)= (5)/(3)`

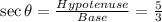
So, for the angle θ,

Hypotenuse = 5 and Base = 3

Using Pythogoras theorem,

(Hypotenuse)² = (Base²) + (Perpendicular )²

(5 )² = ( 3 )² + (Perpendicular )²

⇒ Perpendicular = 25 - 9 = √16 = 4

we have given θ lie in IV quadrant. In IV quadrant cos and sec are positive function but sine, cosec, tan and cot are negative.

`\sin\theta=(Perpendicular)/(Hypotenuse)=-(4)/(5)`

`\cos\theta=(Base)/(Hypotenuse)=(3)/(5)`

`\tan\theta=(Perpendicular)/(Base)=-(4)/(3)`

`\csc\theta=(Hypotenuse)/(Perpendicular)=-(5)/(4)`

`\cot\theta=(Base)/(Perpendicular)=-(3)/(4)`