Question

Sergei buys a rectangular rug for his living room. He measures the diagonal of the rug to be 18 feet. The length of the rug is 3 feet longer than the width.

What are the approximate dimensions of the rug? Round each dimension to the nearest tenth of a foot.

10.4 feet by 7.4 feet
11.1 feet by 8.1 feet
13.4 feet by 10.4 feet
14.1 feet by 11.1 feet

Answer 1

14.1 feet by 11.1 feet is the correct one

Answer 2

D. 14.1 feet by 11.1 feet.

Explanation:

Let w be the width of the rug.

We have been given that the length of the rug is 3 feet longer than the width. So the length of the rug would be
`w+3`.

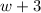We have been given that the measure of the diagonal of the rug to be 18 feet. To find the width of rug we will use Pythagoras theorem as rug is rectangular.

`w^2+(w+3)^2=18^2`

`w^2+w^2+6w+9=324`

`2w^2+6w+9=324`

`2w^2+6w+9-324=0`

`2w^2+6w-315=0`

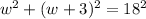
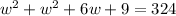
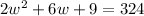
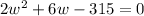
We will use quadratic formula to solve for w.

`w=(-b\pm √(b^2-4ac))/(2a)`

`w=(-6\pm √(6^2-4*2*-315))/(2*2)`

`w=(-6\pm √(36+2520))/(4)`

`w=(-6\pm √(2556))/(4)`

`w=(-6)/(4)\pm (√(2556))/(4)`

`w=(-6)/(4)\pm (50.55689863)/(4)`

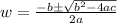
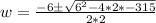
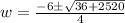
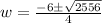
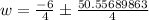
Since the width cannot be negative, so width of the rug would be:

`w=(-6)/(4)+(50.55689863)/(4)`

`w=-1.5+12.639224659`

`w=11.139224\approx 11.1`

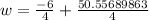
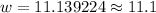
Therefore, the width of rug would be 11.1 feet.

Since length of rug is 3 feet longer than width, so width of the rug would be
`11.1+3=14.1`,

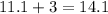Therefore, the option D is the correct choice.