Question

According to the rational root theorem, the numbers below are some of the potential roots of f(x) = 10x3 + 29x2 – 66x + 27. Select all that are actual roots. A) -9/2 B)-9/10 C) 3/5 D) 1 E) 3

Answer 1

-9/2, 3/5, 1

Explanation:

Answer 2

answer : A , C , D

`f(x) = 10x^3 + 29x^2 - 66x + 27`

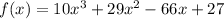
WE plug in each root in f(x) and check whether we get value =0

When f(a) =0 then 'a' is the actual root

Lets start with -9/2, plug in -9/2 for x

`f(x) = 10x^3 + 29x^2 - 66x + 27`

`f(-9/2)= 10((-9)/(2))^3 + 29((-9)/(2))^2 - 66((-9)/(2))+ 27=0`

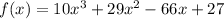
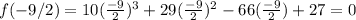
Hence -9/2 is one of the actual root

now plug in -9/10 for x

`f(x) = 10x^3 + 29x^2 - 66x + 27`

`f(-9/10)= 10((-9)/(10))^3 + 29((-9)/(10))^2 - 66((-9)/(10))+ 27=(513)/(5)`

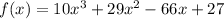
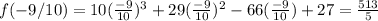
Hence -9/10 is not an actual root

now plug in 3/5 for x

`f(x) = 10x^3 + 29x^2 - 66x + 27`

`f(3/5)= 10((3)/(5))^3 + 29((3)/(5))^2 - 66((3)/(5))+ 27=0`

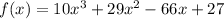
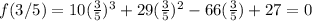
So 3/5 is one of the actual root

Now plug in 1 for x

`f(1) = 10(1)^3 + 29(1)^2 - 66(1)+ 27=0`

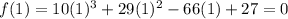
So 1 is one of the actual root

Now plug in 3 for x

`f(3) = 10(3)^3 + 29(3)^2 - 66(3)+ 27=360`

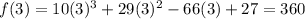
So 3 is not the actual root

Answer is -9/2 , 3/5 and 1