Answer:
All possible rational roots are: 1, 1/3, 2, 2/3, 3, 6.
Explanation:
The given expression is
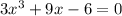
The rational root theorem states the divisors of the constant are possible roots. Additionally, if the term with the greater exponent as a coefficient different than one, then we must incluce its divisor, to then divide them by the divisor of the constant.
According to the theorem, all possible rational roots are
Divisors of 6: 1, 2, 3, 6.
Divisors of 3: 1, 3.
Possible rational roots: 1/1, 1/3, 2/1, 2/3, 3/1, 3/3, 6/1, 6/3.
Therefore, all possible rational roots are: 1, 1/3, 2, 2/3, 3, 6.