Question

Triangle PQR has vertices at P(2, 4), Q(3, 8) and R(5, 4). A similarity transformation maps triangle PQR to triangle ABC, whose vertices are A(2, 4), B(5.5, 18), and C(12.5, 4). What is the scale factor of the dilation in the similarity transformation? a. 2 b. 2.5 c. 4 d. 3.5

Answer 1

Answer: The correct option is (d) 3.5.

Step-by-step explanation: Given that triangle PQR has vertices at P(2, 4), Q(3, 8) and R(5, 4). A similarity transformation maps triangle PQR to triangle ABC, whose vertices are A(2, 4), B(5.5, 18), and C(12.5, 4).

We are to find the scale factor of the similarity transformation.

Scale factor of a dilation is defined as

`S=\frac{\textup{length of a side of the dilated figure}}{\textup{length of the corresponding side of the original figure}}.`

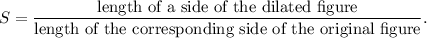
In ΔABC and ΔPQR, the corresponding side of BC is QR.

Now, the lengths of the sides QR and BC are calculated using the distance formula as follows:

`QR=√((5-3)^2+(4-8)^2)=√(4+16)=√(20)=2\sqrt5~\textup{units},\\\\BC=√((12.5-5.5)^2+(4-18)^2)=√(49+196)=√(245)~\textup{units}.`

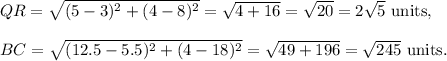
Therefore, the sale factor of dilation from ΔPQR to ΔABC is

`S=(BC)/(QR)=(√(245))/(2\sqrt5)=(√(49))/(2)=(7)/(2)=3.5.`

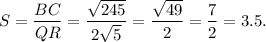
Thus, the required scale factor is 3.5.

Option (d) is correct.