Question

Given a soda can with a volume of 15 and a diameter of 2, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank).

Answer 1

Answer: 5 cube unit

Explanation:

Since, The volume of a cylinder having radius r and height h

=
`\pi r^2h`

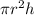
The volume of a cone having radius r and height h

=
`(1)/(3)\pi r^2h`

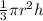
Here, the shape of the cone is cylindrical,

And, the diameter of the cylinder = 2 unit,

⇒ The radius of the cylinder = 1 unit,

Let h be the height of the cylinder,

⇒
`\text{ The volume of the cylinder } = \pi (1)^2 h`

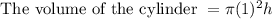
According to the question,

`\pi h = 15`

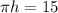
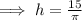`\implies h = (15)/(\pi)` unit.

Now, the largest cone that can be fit inside the given can must have the same height as the can,

⇒
`\text{ The height of the largest cone} = (15)/(\pi)`

Also, the cone must have the same diameter or radius as the can,

⇒ The radius of the largest cone inside the can = 1 unit,

⇒
`\text{ The volume of the largest cone } = (1)/(3)\pi (1)^2((15)/(\pi))`

`=(15\pi)/(3\pi)`

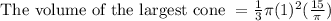
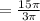
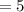`=5` cube unit