Question

Which statement about the asymptotes is true with respect to the graph of this function?

O The horizontal asymptotes lies at x 1 and x
O The vertical asymptotes are x 3 and x
O The graph crosses the horizontal asymptote.
O The graph has two vertical asymptotes and one horizontal
asymptote.

Answer 1

When you graph the equation you notice that there is 2 vertical and 1 horizontal asymptote. or D

Answer 2

Option D.

Explanation:

The given function is

`f\left(x\right)=(3x^(2)-3)/(x^(2)-4)`

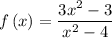
In this function the degree of numerator an denominator is same i.e., 2.

Horizontal Asymptotes: If the degree of numerator an denominator is same, then

`\text{Horizontal asymptote}=\frac{\text{Leading coefficient of numerator}}{\text{Leading coefficient of denominator}}`

`\text{Horizontal asymptote}=(3)/(1)`

`\text{Horizontal asymptote}=3`

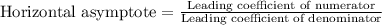
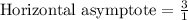
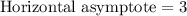
Horizontal asymptote is y=3.

`f(x)=3`

`(3x^(2)-3)/(x^(2)-4)=3`

`3(x^(2)-1)=3(x^(2)-4)`

`x^(2)-1=x^(2)-4`

`1=4`

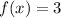
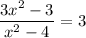
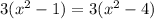
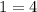
This statement is false for any value of x, therefore the graph does not cross the horizontal asymtote.

Vertical Asymptotes: Equate the denominator equal to 0, to find the vertical asymptotes.

`x^2-4=0`

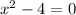
Add 4 on both sides.

`x^2=4`

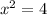
Taking square root on both sides.

`x=\pm √(4)`

`x=\pm 2`

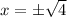
Vertical asymptotes are x=2 and x=-2.

The graph has two vertical asymptotes and one horizontal asymptote.

Therefore, the correct option is D.