Question

Lisa invests $4,000 in two types of bonds, bond A and bond B. Bond A offers a 10% return, and bond B offers a 6% return. Lisa invests $x in bond A and $y in bond B. Her total return on the investment is $340.

The system of linear equations defining the situation is . The amount Lisa invested at the rate of 10% is , and the amount she invested at the rate of 6% is .

Answer 1

x+y=4000....(1)
10x+6y=340*100⇒5x+3y=17000......(2)

(2)- 3*(1)⇒ 2x=5000⇒x=2500,y=4000-2500=1500

Answer 2

Answer: The amount invested at the rate of 10% is $2500 and that of 6% is $1500.

Step-by-step explanation: Given that Lisa invests $4,000 in two types of bonds, bond A and bond B. Bond A offers a 10% return, and bond B offers a 6% return.

Lisa invests $x in bond A and $y in bond B and her total return on the investment is $340.

According to the given information, the system of linear equations can be written as

`x+y=4000~~~~~~~~~~~~~~(i)\\\\10\%* x+6\%* y=340\\\\\\\Rightarrow (10)/(100)x+(6)/(100)y=340\\\\\\\Rightarrow (x)/(10)+(3x)/(50)=340\\\\\\\Rightarrow (5x+3y)/(50)=340\\\\\Rightarrow 5x+3y=17000~~~~~~~~~~~~~~(ii)`

Multiplying equation (i) by 5, we have

`5x+5y=20000~~~~~~~~~~~~~~~~(iii)`

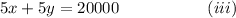
Subtracting equation (ii) from equation (iii), we get

`(5x+5y)-(5x+3y)=20000-17000\\\\\Rightarrow 2y=3000\\\\\Rightarrow y=1500,`

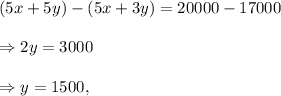
and from equation (i), we get

`x=4000-1500=2500.`

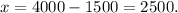
Thus, the system of linear equations defining the situation is

`x+y=4000\\\\5x+3y=17000,`

and

the amount Lisa invested at the rate of 10% is $2500 and the amount she invested at the rate of 6% is $1500.