Question

How to use series to find definite integral?

Answer 1

Given


`\displaystyle\int_a^bf(x)\,\mathrm dx`

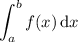
you can evaluate the integral by first expanding
`f(x)` as a series, say


`\displaystyle\int_a^b\sum_(n\ge0)c_nx^n\,\mathrm dx`

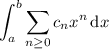
then interchange the order of integration/summation (provided Fubini's theorem holds; it usually will, so no need to worry greatly about this aspect) to write


`\displaystyle\sum_(n\ge0)c_n\int_a^bx^n\,\mathrm dx`

Then evaluating the integral yields


`\displaystyle\sum_(n\ge0)c_n(x^(n+1))/(n+1)\bigg|_(x=a)^(x=b)`

`\displaystyle\sum_(n\ge0)c_n(b^(n+1)-a^(n+1))/(n+1)`

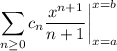
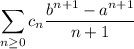
Given an appropriate sequence
`c_n`, you would then be able to evaluate the integral exactly, or at the very least find a partial sum that approximates the value of the integral to within a specified degree of accuracy.

Here's an example that demonstrates the procedure. Suppose we want to evaluate the definite integral


`\displaystyle\int_0^1\sin\pi x\,\mathrm dx`

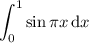
Recall that


`\sin x=\displaystyle\sum_(n\ge0)((-1)^nx^(2n+1))/((2n+1)!)`

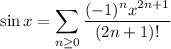
so that we can write the definite integral as


`\displaystyle\int_0^1\sin\pi x\,\mathrm dx=\int_0^1\sum_(n\ge0)((-1)^n(\pi x)^(2n+1))/((2n+1)!)\,\mathrm dx=\sum_(n\ge0)((-1)^n\pi^(2n+1))/((2n+1)!)\int_0^1x^(2n+1)\,\mathrm dx`

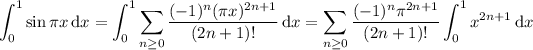
Integrating yields


`\displaystyle\int_0^1x^(2n+1)\,\mathrm dx=(x^(2n+2))/(2n+2)\bigg|_(x=0)^(x=1)=\frac1{2n+2}`

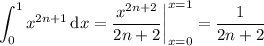
and so we're left with


`\displaystyle\sum_(n\ge0)((-1)^n\pi^(2n+1))/((2n+2)(2n+1)!)=\sum_(n\ge0)((-1)^n\pi^(2n+1))/((2n+2)!)`

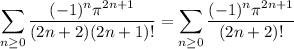
The trick now is to evaluate the sum. Well, recall that


`\cos x=\displaystyle\sum_(n\ge0)((-1)^nx^(2n))/((2n)!)`

Our sum closely resembles this power series. In our sum, we have odd powers of
`\pi` in the numerator, but even factorials in the denominator. We can adjust for this by simply multiplying by
`\frac\pi\pi`:


`\displaystyle\sum_(n\ge0)((-1)^n\pi^(2n+1))/((2n+2)!)=\frac1\pi\sum_(n\ge0)((-1)^n\pi^(2n+2))/((2n+2)!)`

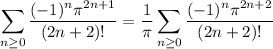
Now, our denominators take the form
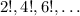
`2!,4!,6!,\ldots`, while the cosine series proceeds with
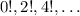
`0!,2!,4!,\ldots` - in other words, our sum skips the first term of the cosine series. We can adjust for this as well, by adding and subtracting the same term of
`1`. In terms of our summand, we can get
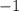
`-1` by plugging in
`n=-1`, so we can write


`\displaystyle\frac1\pi\left(-1+1+\sum_(n\ge0)((-1)^n\pi^(2n+2))/((2n+2)!)\right)=\frac1\pi\left(1+\sum_(n\ge-1)(-1)^n\pi^(2n+2))/((2n+2)!)\right)`

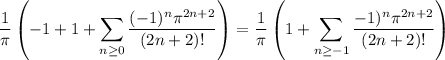
Then shifting the index by 1 so that it starts at
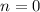
`n=0` gives


`\displaystyle\frac1\pi\left(1+\sum_(n\ge0)((-1)^(n+1)\pi^(2n))/((2n)!)\right)`

and now our sum exactly resembles to the negated cosine series evaluated at
`x=\pi`.


`\displaystyle\frac1\pi\left(1+\underbrace{\sum_(n\ge0)((-1)^(n+1)\pi^(2n))/((2n)!)}_(-\cos\pi)\right)=\frac1\pi(1-\cos\pi)=\frac1\pi(1-(-1))=\frac2\pi`

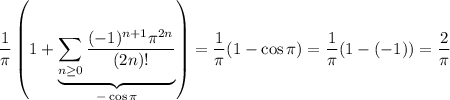
We can verify that this result is correct:


`\displaystyle\int_0^1\sin\pi x\,\mathrm dx=\frac1\pi\int_0^1\sin\pi x\,\mathrm d(\pi x)=-\frac1\pi\cos \pi x\bigg|_(x=0)^(x=1)=-\frac1\pi(\cos\pi-\cos0)=\frac2\pi`