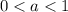Question

Suppose the graph of the parent function y=cot(x) is vertically compressed to produce the graph of the function y=a cot(x) but there are no reflections. Which describes the value of a? a. a<-1 b. -1 c. 0 d. a>1

Answer 1

Dang...I literally had this question in Algebra the other day, and got it wrong....but i believe the actual answer was B. It was for sure not D XD. Sorry if I am wrong yet again.

Answer 2

The required value of a is
`0<a<1`

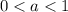
Explanation:

Given : Suppose the graph of the parent function
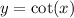`y=\cot(x)` is vertically compressed to produce the graph of the function
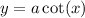`y=a\cot(x)` but there are no reflections.

To find : Which describes the value of a?

Solution :

When the graph is vertically compressed by unit a

then the value of a lies between
`0<a<1`

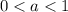
So, In the graph of parent function
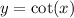`y=\cot(x)` is vertically compressed to produce the graph of the function
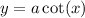`y=a\cot(x)` the value of a lies between
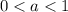`0<a<1` as there is no reflection so no changes.

Therefore, The required value of a is
`0<a<1`