Answer with Step-by-step explanation:
We are given that a triangle ABC. In triangle ABC , the coordinates of A is at (0,0), Point B is at
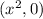 , Point C is at
, Point C is at
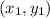 , Point D is at
, Point D is at
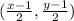 , Point E is at
, Point E is at
![(\frac{x-1(x-2)/(2),(y-1)/(2))]() .
.
The coordinates of point E can be write as
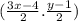 .
.
Slope formula of a line passing through two points
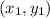 and
and
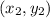 is given by
is given by
=
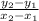 .
.
By using slope formula of a line
Slope of line AB which passing through the points A (0,0) and B
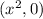
Where
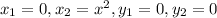
=
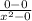
Slope of line AB which passing through the points A(0,0) and B
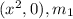 =0
=0
Slope of line DE which passing through the points D
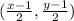 and E
and E
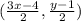
Where

=

Slope of line DE,
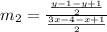
Slope of line DE,
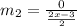
Slope of line DE which passing through the points D
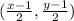 , and E
, and E
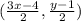
=0
We know that when two lines are parallel then thier slopes are equal.
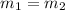
Slope of line DE = Slope of line AB
Hence, the line DE and line AB are parallel lines.