If the perimeter is 122.4 cm, then the length of WZ is
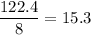
, which means YZ has length
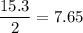
, so the first option is not true.
The radius of the octagon is XZ = 20 cm, and the apothem is XY. If we had the length of XY, we can determine whether the second option is true, so let's skip ahead to the third for a moment.
The third option is indeed true and follows from the Pythagorean theorem, so that
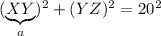
We know YZ = 7.65 cm, so we have
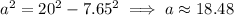
Back to the second option: the measure of angle ZXY (between the radius XZ and the apothem XY) satisfies
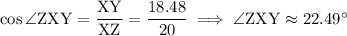
which means the second option is not true. (In fact, the angle measure should be exactly 22.5 degrees, but my calculator is carrying approximations from when we solve for

.)
The fourth option is false, because we already know WZ = 15.3.
Finally, option 5 is true. The central angle is 1/8 of a full revolution, which means the angle has measure
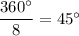
, as stated.
So to recap:
False
False
True
False
True