Question

Determine the total number of roots of each polynomial function.

f (x) = 3x6 + 2x5 + x4 - 2x3

Answer 1

Base on my research there are ways to get the number of roots. If you are looking for negative roots and even the positive one has their own ways. But in this problem, we just need to determine the total number of roots of a polynomial. In determining the total number of roots, you just need to find the degree of the polynomial function. The degree refers to the highest exponent of the polynomial. Therefore, in the function given, 6 is the degree of the polynomial function. The total number of roots is 6. 

Answer 2

For this case we have the following function:

`image`

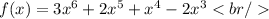
The first thing that we must observe to know the amount of roots that the function has, is the degree of the greatest exponent.

We observe that the degree of the greatest exponent is equal to 6.

Therefore, the function has 6 roots.

The roots can all be real with different multiplicities.

There may also be real roots and complex roots.

Answer:

The total number of roots for the given polynomial function is 6.