Question

Two angles of a triangle have equal measures, but the third angle's measure is 36° less than the sum of the other two. Find the measure of each angle of the triangle. The first and second angles measure degrees, and the third angle measures degrees.

Answer 1

54,54,72

X+X+2X-36=180
4X-36=180
4X= 216
Divide by 4
X= 54
X=54
2(54)-36=72

Answer 2

Answer: The first and second angles measure 54 degrees, and the third angle measures 72 degrees.

Step-by-step explanation: Given that two angles of a triangle have equal measures, but the third angle's measure is 36° less than the sum of the other two.

We are to find the measure of each angle of the triangle.

Let, x° be the measure of each of the two angles that has equal measure.

Then, the measure of the third angle will be (x° + x° - 36°) = (2x° - 36°).

From Angle-Sum-Property of a triangle, we have

`x^\circ+x^\circ+(2x^\circ-36^\circ)=180^\circ\\\\\Rightarrow 2x^\circ+2x^\circ-36^\circ=180^\circ\\\\\Rightarrow 4x^\circ=180^\circ+36^\circ\\\\\Rightarrow 4x^\circ=216^\circ\\\\\Rightarrow x=54^\circ.`

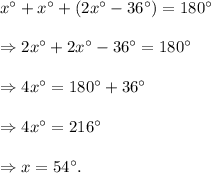
So, the measure of each angle of equal measure is 54°, and the measure of the third angle is

`2* 54^\circ-36^\circ=108^\circ-36^\circ=72^\circ.`

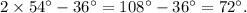
Thus, the first and second angles measure 54 degrees, and the third angle measures 72 degrees.