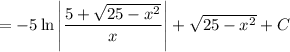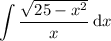
Setting
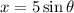
, you have

. Then the integral becomes
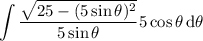
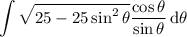

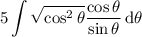
Now,
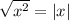
in general. But since we want our substitution
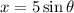
to be invertible, we are tacitly assuming that we're working over a restricted domain. In particular, this means
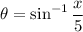
, which implies that
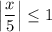
, or equivalently that
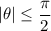
. Over this domain,
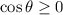
, so
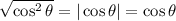
.
Long story short, this allows us to go from
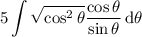
to
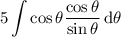
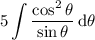
Computing the remaining integral isn't difficult. Expand the numerator with the Pythagorean identity to get
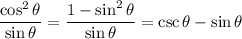
Then integrate term-by-term to get


Now undo the substitution to get the antiderivative back in terms of

.
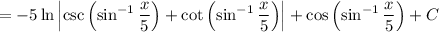
and using basic trigonometric properties (e.g. Pythagorean theorem) this reduces to