Question

Lim x-->+ infinity (2^x)/x^10

Answer 1

`\displaystyle\lim_(x\to\infty)(2^x)/(x^(10))=\lim_(x\to\infty)(e^(x\ln2))/(x^(10))=\frac\infty\infty`

A few applications of L'Hopital's rule gives a decent idea of how this limit will ultimately behave.


`=\displaystyle\lim_(x\to\infty)(\ln2\,e^(x\ln2))/(10x^9)`

`=\displaystyle\lim_(x\to\infty)((\ln2)^2\,e^(x\ln2))/(90x^8)`

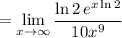
and so on. Notice that the numerator will consistently behave exponentially, while the denominator will eventually be rendered into a constant. This means the function diverges to
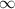
`\infty` as
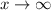
`x\to\infty`.