Answer:
Explanation:
Alright, lets get started.
using Sine Law,
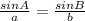
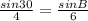
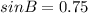

Another angle will be
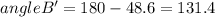
considering angle B, angle C =
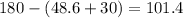
considering angle B', angle C' =
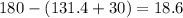
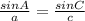
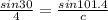

Similarly, finding c'
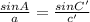


Hence two triangles are possible with below details: : Answer
A = 30, B = 48.6, C = 101.4, c = 7.84
A = 30, B' = 131.4, C' = 18.6, c' = 2.55
Hope it will help :)