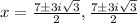Question

What is the solution of the equation (x – 5)2 + 3(x – 5) + 9 = 0? Use u substitution and the quadratic formula to solve.

Answer 1

(x - 5)2 + 3(x - 5) + 9 = 0

Simplify.

2x - 10 + 3x - 15 + 9 = 0

Add like terms.

(2x + 3x) + (-10 - 15 + 9) = 0

Simplify.

5x + (-34) = 0

5x - 34 = 0

Add 34 to both sides.

5x = 0 + 34

5x = 34

Divide both sides by 5.

x = 34/5

So, x = 6 4/5

~Hope I helped!~

Answer 2

The solution of the equation is
`x=(7\pm 3i√(3))/(2),(7\pm 3i√(3))/(2)`

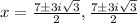
Explanation:

Given : Equation
`(x -5)^2 + 3(x -5) + 9 = 0`

To find : What is the solution of the equation?

Solution :

We have given the expression in quadratic form
`ax^2+bx+c=0`

Let
`(x-5)=u` .....(10

The equation form is
`u^2 + 3u + 9 = 0`

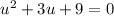
The solution of a quadratic formula is,
`x=\frac{-b\pm√(b^2-4ac)} {2a}`

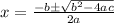
On comparing with general form,

a=1 ,b=3, c=9

Substitute in the formula,

`u=(-3\pm√(3^2-4(1)(9)))/(2(1))`

`u=(-3\pm√(9-36))/(2)`

`u=(-3\pm√(-27))/(2)`

`u=(-3\pm 3√(3)i)/(2)`

`u_1=(-3+3√(3)i)/(2)`

`u_2=(-3-3√(3)i)/(2)`

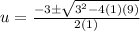
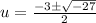
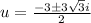
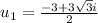
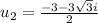
Substitute in equation (1),

`x-5=u_1`

`x-5=(-3+3√(3)i)/(2)`

`x=(-3+3√(3)i)/(2)+5`

`x=(7\pm 3i√(3))/(2)`

`x-5=u_2`

`x-5=(-3-3√(3)i)/(2)`

`x=(-3-3√(3)i)/(2)+5`

`x=(7\pm 3i√(3))/(2)`

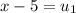
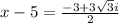
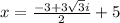
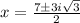
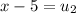
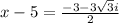
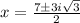
Therefore, The solution of the equation is
`x=(7\pm 3i√(3))/(2),(7\pm 3i√(3))/(2)`