Question

Line L has equation 2x - 3y = 5. Line M passes through the point (2, -10) and is perpendicular to line L. Determine the equation for line M.

A) 2x + 3y = -14 B) 2x - 3y = -26 C)3x + 2y = -14 D) 3x - 2y = -26

Answer 1

C has to be the right one

Answer 2

Option C is correct.

Explanation:

Given Equation of Line L is 2x - 3y = 5

Line M is perpendicular to line L and Line M passes through point ( 2 , -10 )

first rewrite equation of line L in slope intercept form to get slope of line L,

`2x-3y=5`

`3y=2x-5`

`y=(2)/(3)x-(5)/(3)`

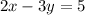
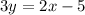
By comparing with , y = mx + c

Slope of line L =
`(2)/(3)`

let slope of M = m1

We know that Product of slope of perpendicular lines equal to -1

So, m × m1 = -1

`(2)/(3)* m1=-1`

`m1=-1*(3)/(2)`

`m1=(-3)/(2)`

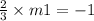
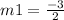
Now we find Equation of Line M using slope and point form,

`y-y_1=m(x-x_1)`

`y-(-10)=(-3)/(2)(x-2)`

`y+10=(-3x+6)/(2)`

`2y+20=-3x+6`

`3x+2y+14=0`

`3x+2y=-14`

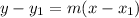
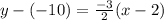
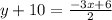
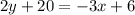
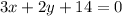
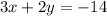
Therefore, Option C is correct.