Question

Which statement completes the proof that the sum of the angles of triangle PRQ is 180°? Statement Justification

Angle 5 is congruent to angle PQR. Alternate Interior Angles Theorem
Angle 1 is congruent to angle PRQ. Alternate Interior Angles Theorem
m∠1 + m∠RPQ + m∠5 = 180° Definition of a Straight Angle and
Straight Angle Postulate
? Substitution

Answer 1

m∠1 + m∠RPQ + m∠5 = 180° Definition of a Straight Angle

proof : mes1= PRQ (alternate interior)

RPQ = 3 Opposite angle (vertex)
5 =Q (alternate interior)
PRQ + RPQ + RQP = 180

Answer 2

The step missing is

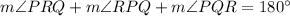`m\angle PRQ + m\angle RPQ + m\angle PQR = 180\°`, by substitution.

Explanation:

We have

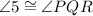`\angle 5 \cong \angle PQR` by Alternate Interior Angles Theorem.

`\angle 1 \cong \angle PRQ`, by Alternate Interior Angle Theorem.

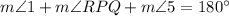`m\angle 1 + m\angle RPQ + m\angle 5 =180\°`, by Definition of a Straight Angle and a Straight Angle postulate.

`\therefore`

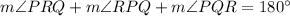`m\angle PRQ + m\angle RPQ + m\angle PQR = 180\°`, by substitution.

Now, remember that Alternate Interior Angles are those which are inside two parallels and different sides of the transversal line which intercept those parallels. Their theorem states that such angles are always congruent.

Then, the definition of a straight angle is that measures 180°, and its postulate is that adjacent angles on an straight angle must sum 180°, and they are supplementary.