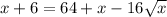Question

Which equation results from isolating a radical term and squaring both sides of the equation for the equation ?

Answer 1

Hence, the desired equation is:

`x+6=64+x-16√(x)`

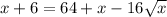
Explanation:

We are given a equation as:

`√(x+6)+√(x)=8`

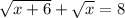
We can also write this equation as i.e. we can isolate our radical term as:

`√(x+6)=8-√(x)`

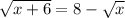
Now on squaring both side of the equation we get:

`(√(x+2))^(2)=(8-√(x))^2`

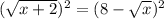
We know that:

`(a-b)^2=a^2+b^2-2ab`

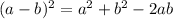
so, we get from the equation:

`x+6=8^2+(√(x))^2-2* 8* √(x)\\\\x+6=64+x-16√(x)`

Hence, the desired equation which is obtained as a result from isolating a radical term and squaring both sides of the equation for the equation is:

`x+6=64+x-16√(x)`