Question

Can anyone explain those marked steps in case (iii)

Answer 1

`\cos\frac{3x}2=\cos\left(\frac\pi2+\frac x2\right)`

`\implies \frac{3x}2=2n\pi+\frac\pi2+\frac x2`

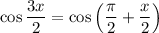
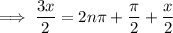
follows from the fact that the cosine function is
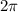
`2\pi`-periodic, which means
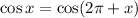
`\cos x=\cos(2\pi+x)`. Roughly speaking, this is the same as saying that a point on a circle is the same as the point you get by completing a full revolution around the circle (i.e. add
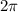
`2\pi` to the original point's angle with respect to the horizontal axis).

If you make another complete revolution (so we're effectively adding
`4\pi`) we get the same result:
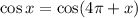
`\cos x=\cos(4\pi+x)`. This is true for any number of complete revolutions, so that this pattern holds for any even multiple of
`\pi` added to the argument. Therefore
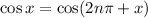
`\cos x=\cos(2n\pi+x)` for any integer
`n`.

Next, because
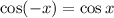
`\cos(-x)=\cos x`, it follows that
`\cos x=\cos(2n\pi-x)` is also true for any integer
`n`. So we have


`\implies \frac{3x}2=2n\pi\pm\left(\frac\pi2+\frac x2\right)`

The rest follows from considering either case and solving for
`x`.