Question

A pizza restaurant has 21 topping choices and 3 crust choices. How many different 3-topping pizzas can be made if toppings can be selected more than once?

Answer 1

it is 27, 783. Hope this helps

Answer 2

Answer: 27783

Explanation:

Given : The number of toppings for pizza= 21

If repetition of toppings is allowed, then the number of different 3-topping combinations will be :-

`21*21*21=9261`

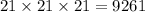
Also, the number of choices for crust = 3

Then, the number if different 3-topping pizzas can be made if toppings can be selected more than once will be :_

`9261*3=27783`

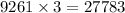
Hence, the number of different 3-topping pizzas can be made = 27783