Question

Solve sqrt 3 cot theta +1 = 0

Answer 1

Solve:
`√(3)cot\theta + 1 = 0`

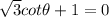
Recall that cot(x) really is just 1/tan(x).

Thus, we can say:
`(√(3))/(tan\theta) + 1 = 0`

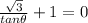
Isolate the variable to solve directly for theta.

`(√(3))/(tan\theta) = -1`

`√(3) = -tan\theta`

`tan\theta = -√(3)`


`\theta = tan^(-1)(-√(3))`

`\theta = -(\pi)/(3)`

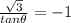
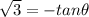
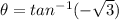
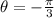
However, that's not the only solution:
For instance,
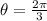
`\theta = (2\pi)/(3)` is another solution.
In fact, there are an infinite amount of solutions we can have that will satisfy this equation because of the fact that the tangent wave is periodic every π.

Thus, we can say for every π periods, we will have a solution.
Or:
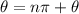
`\theta = n\pi + \theta`, where
`n \in \mathbb{R}`

By substituting Θ, we can say that the solutions are:

`\theta = n\pi - (\pi)/(3)`, where
`n \in \mathbb{R}`