Question

Ah! Okay, need help solving 14, and just checking for 16 and 4.

4. I got the series is Divergent by Root Test because you get e > 1

14. I was thinking Maclaurin Series? But it isn't working out properly?

16. I need to find a power series representation and interval of convergence for the given series. I found the power series representation to be:
(-1)^n(n+1)x^n and the lim by Ratio Test comes to abs value of x. Should I be testing endpoints?

Answer 1

4. Correct. You also could have used the limit test for divergence for the same conclusion (the summand approaches infinity).

- - -

14. I'm guessing the instructions are the same as for 16. Rewrite as


`f(x)=\frac4{2x+3}=\frac{\frac43}{1-\left(-\frac{2x}3\right)}`

Now recall that for
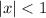
`|x|<1`, we have


`\frac1{1-x}=\displaystyle\sum_(n\ge0)x^n`

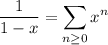
so that for this function, we get


`f(x)=\frac43\displaystyle\sum_(n\ge0)\left(-\frac{2x}3\right)^n`

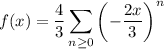
Because this is a geometric sum, this converges when
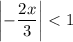
`\left|-\frac{2x}3\right|<1`, or
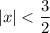
`|x|<\frac32`. This would be the interval of convergence.

Your hunch about checking the endpoints is correct. Checking is easy in this case, because at the endpoints (-3/2 and 3/2) the series obviously diverges.

- - -

16. This one is kind of tricky, and there's more than one way to do it. The standard method would be to take the antiderivative:


`F(x)=\displaystyle\int f(x)\,\mathrm dx=\int(\mathrm dx)/((1+x)^2)=-\frac1{1+x}+C`

We also have


`\displaystyle-\frac1{1+x}=-\frac1{1-(-x)}=-\sum_(n\ge0)(-x)^n\implies F(x)=C-1-\sum_(n\ge1)(-x)^n`

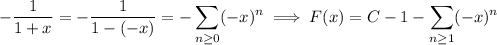
and differentiating this gives


`f(x)=-\displaystyle\sum_(n\ge1)n(-x)^(n-1)=-\sum_(n\ge0)(n+1)(-x)^n=\sum_(n\ge0)(n+1)(-1)^(n+1)x^n`

By the ratio test, this converges when


`\displaystyle\lim_(n\to\infty)\left|((n+2)(-1)^(n+2)x^(n+1))/((n+1)(-1)^(n+1)x^n)\right|<1`

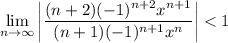
The limit reduces to


`\displaystyle|x|\lim_(n\to\infty)(n+2)/(n+1)=|x|`

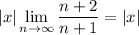
and so the series converges absolutely for
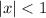
`|x|<1`. Checking the endpoints is also easy in this case. The factor of
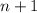
`n+1` is a clear sign that the series will diverge at either extreme.