Question

How do you know where to put the constant when finding general solutions for differential equations?

Answer 1

Let's suppose we want to solve
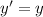
`y'=y` with
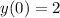
`y(0)=2`. Separating variables and integrating, we get


`\displaystyle\int\frac{\mathrm dy}y=\int\mathrm dx\implies\ln|y|=x+C\implies y=e^(x+C)`

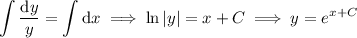
Leaving the solution in this form, the initial condition gives


`2=e^(0+C)=e^C\implies C=\ln2`

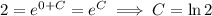
This means the solution is
`y=e^(x+\ln2)`.

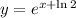
Now if we were to write
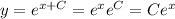
`y=e^(x+C)=e^xe^C=Ce^x`, then we would have found


`2=Ce^0\implies C=2`

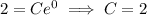
so that the solution would have been
`y=2e^x`.

But these two solutions are the same, since
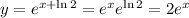
`y=e^(x+\ln2)=e^xe^(\ln2)=2e^x`. So we get the same solution regardless of where we place
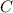
`C`, despite getting different values for
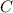
`C`.