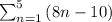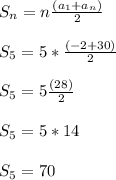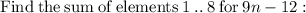
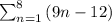

.....
Its an arithmetic sequence
"An arithmetic sequence is an ordered series of numbers, in which the change in numbers is constant"
To determine whether you have an arithmetic sequence, find the difference between the first few and the last few numbers. Ensure that the difference is always the same.
For example, the series 10, 15, 20, 25, 30 is an arithmetic sequence, because the difference between each term is constant (5).
The sequence is
-3, 6, 15...... the difference between each term is contant (9)
Now, identify the first and last terms in the sequence you need to know both of these numbers in order to calculate the sum of the arithmetic sequence.
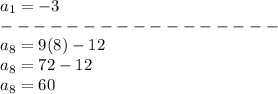
The formula for finding the sum of an arithmetic sequence is
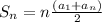
where
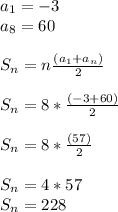
****************************************************************************
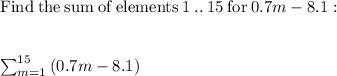

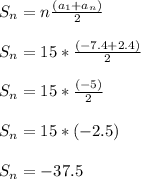
**************************************************************************