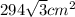Question

The base of a regular pyramid is a hexagon. What is the area of the base of the pyramid? (Express your answer in radical form)

Answer 1

Since angle c is 30° the side lengths of the hexagon are 14 cm as well, which is always true of hexagons because if you divide the hexagon into six triangle they are all equilateral triangles...the area of any regular polygon can be expressed as:

A(n,s)=ns^2/(4tan(180/n)), n=number of sides, s=side length...in this case:

A(6,14)≈509.22 cm^2

Answer 2

Formula for Sine ratio:

`\sin \theta = \frac{\text{Opposite side}}{\text{Adjacent side}}`

As per the statement:

labelled the diagram as shown below

The base of a regular pyramid is a hexagon as shown in the diagram.

Let s be the side of the regular hexagon.

Using sine ratio on triangle ABC

`\sin 60^(\circ) = (a)/(14)`

⇒
`(√(3))/(2)= (a)/(14)`

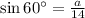
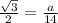
Multiply both sides by 14 we have;

⇒
`7√(3) = a`

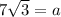
or

`a = 7√(3)` cm

Using Pythagoras theorem.

`\text{Hypotenuse side}^2 = \text{opposite side}^2+\text{Adjacent side}^2`

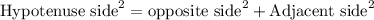
Apply the Pythagoras theorem to ABC:

`14^2 = (7√(3))^2+(BC)^2`

⇒
`196 = 147+BC^2`

⇒
`49 = BC^2`

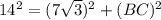
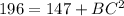
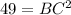
Simplify:

`BC = √(49) = 7`

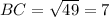
AD = 2 BC

⇒
`s = 2 \cdot 7 = 14 cm`

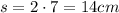
Area of the regular hexagon(A) is given by:

`A =(3√(3))/(2)s^2`

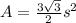
where, s is the side of the regular hexagon.

Substitute the given values we have;

`A=(3√(3))/(2) \cdot 14 \cdot 14 = 3√(3) \cdot 7 \cdot 14= 294√(3) cm^2`

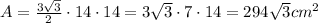
Therefore, the area of the base of the pyramid is,
`294√(3) cm^2`