Question

Test for convergence

Answer 1

You've established that


`\displaystyle\sum_(n\ge1)\frac1{2^n}\le\int_1^\infty(\mathrm dx)/(2^x)`

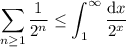
so all you need to do is compute the integral. Rewrite the integrand as


`\frac1{2^x}=2^(-x)=e^{\ln2^(-x)}=e^(-x\ln2)`

and replace
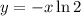
`y=-x\ln2`, so that
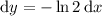
`\mathrm dy=-\ln2\,\mathrm dx`. Then


`\displaystyle\int_(x=1)^(x\to\infty)(\mathrm dx)/(2^x)=\int_(y=-\ln2)^(y\to-\infty)e^y\,(\mathrm dy)/(-\ln 2)=\frac1{\ln2}\int_(-\infty)^(-\ln2)e^y\,\mathrm dy`

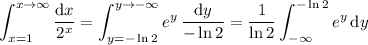
By the fundamental theorem of calculus, this evaluates to


`\frac1{\ln2}e^y\bigg|_(y\to-\infty)^(y=-\ln2)=\frac1{\ln2}\left(e^(-\ln2)-\lim_(y\to-\infty)e^y\right)=(e^(-\ln2))/(\ln2)=(\frac12)/(\ln2)=-\frac1{2\ln2}=\frac1{\ln4}`

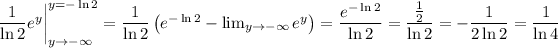
and so the series converges.

You also could have used the fact that the series is geometric with common ratio less than 1 to arrive at the same conclusion, with the added perk of being able to find the exact value of the sum to corroborate this.