Question

A new car that sells for $21,000 depreciates (decreases in value) 16% each year. Write a function that models the value of the car. Find the value of the car after 3 years.

Answer 1

A=p(1-r)^t
A=21,000×(1−0.16)^(3)
A=12,446.784=12447

Answer 2

Answer: a)
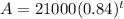`A=21000(0.84)^t`, where 'A' is the value of car after 't' years.

b) $12446.784

Explanation:

Given: A new car that sells for $21,000 depreciates (decreases in value) 16% each year.

Then a function that models the value of the car will be

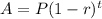`A=P(1-r)^t`, where 'P' is the selling price of car, 'r' is the rate of depreciation in decimal, 't' is the time in years and 'A' is the value of car after 't' years.

Thus after substituting given value, the function becomes

`A=21000(1-0.16)^t\\=A=21000(0.84)^t`

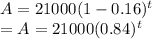
To find the value after 3 years, substitute t=3 in the above function.

`A=21000(0.84)^3=12446.784`

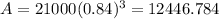
Hence the value of car after 3 years=$12446.784